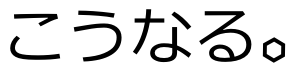favorites of q7ny3v
Re: 春の風
これ、たまに思います。 |
返信 |
Reply 思考の泡 Quote | |
私が死んでも何も変わらないが、私が死ぬことで、変わる何かが未来にはあるのだろうか。あるいは、私が生きて春を迎え続けることで、何か良いことでも起こるのだろうか。
起こるはずだと信じたい私の気持ちは、できれば速やかに廃棄されたいと言う気持ちと矛盾している。
ほんと、そうだ。
どう言い換えても変わらない、ほんと、そうだ。
関連
以下蛇足。
もう数年前だろうか。角膜だかどこだったか、とにかく、「パーツとしての」最長寿記録が更新された、ってニュースを何かで読んだことがある。
移植することで機能し続けたパーツがある、って話だったと思う。細かい数字は覚えてないけど、まあ例えば70歳で死んだ人の角膜を移植された人がその後60年生きたら、パーツとしては130年生きたよね、みたいな話。
命って何だろう、って、たまに思う。オレどうせ子孫残さないしな。
Re: より、変態らしく
Re: それ、これですか
Re: それ、これですか
http://c9zchq.sa.yona.la/257 |
返信 |
明日面接を受けにいくことになってる。
今日は温かくて気持ちいいのに、明日は気温が10度も下がるらしい。
面接なんてもうしばらく受けてない。明日は外に出る。普段着でいいって。
Amazonで新しいキーホルダーを買ったからお守りに持っていく。
僕はそういうのが好きだから。気持ちがちょっと上を向くから。
Re: 無限とか永遠とか
それ、これですか |
返信 |
Reply 思考の泡 | |
大きいのと小さいのの円周が同じ！ふしぎ！
もしこれなら、オレもあれっと思ったんですけど、そうでなくてこういうのを作って、これを床に置いて転がして真っすぐ走らせるにはどっちかが滑ってないとだめじゃん、と思ったら納得できました。
いやいや床に置いたら高さが違っちゃうじゃん軸が傾くじゃん、ということなら、だったら軸が水平になるように床の方を傾けて真横から見れば同じことじゃん、って。
デフギア考えた人って頭いいなあ、って、何度見ても思います。
無限とか永遠とかって、底の見えない井戸を覗き込んで身を乗り出して「わっ怖ぇ！こっっっうぇ！！」ってやってる小学生なんかと同じで（オレにとっては）、いくつになっても、怖いもの見たさ。
オレ、大きくなったら、この中学いってこの先生に習うんだ…
http://c9zchq.sa.yona.la/255 |
返信 |
思春期の中学生にパイを教える数学教師の気持ちはどんなものなんだろう。
これがパイです。新任の女教師が黒板にチョークで丁寧にパイの記号を刻む。
そしてこれが私の2パイR。黒のリクルートスーツに映える先生の控え目な桜吹雪。
Re: それはとっても嬉しいなって
円環の理に導かれて七等分されるんですね、わかります。 |
返信 |
Reply | |
ハートフルで気の効いた返信をしようとモニタの前で30分粘りましたが、何も出て来ませんでした。
えーっと・・・奇跡も、魔法も、あるんだよ？
無限とか永遠とか |
返信 |
ここ数日、円周率にまつわる話が盛り上がっているようですね。
なんかうらやましい。私は未だに、「内側の車輪が"滑っている"」の話がイマイチ理解出来ん…。
(内側の車輪(内径・小さい)と外側の車輪(外径・大きい)が動く距離が同じであるというヤツ)
大分昔だけど、円周率とか無限とか、そういうのに妙にあこがれた時期がありました。
子どものころじゃなくて、十分大人になってからなんだけど。
十分大人だったころが大分昔っていうのも、何か嫌だな。ちょっと前ってことにしよう…。
当時、どこだかでマンデルブロ曲線だかなんだか言う図形を描くフリーソフトを見つけて、
時折起動しては、サイケデリックな図形が生まれていくのを楽しんでいました。
サイケだと思ったのは、使われている色がフューシャピンクとか、そういう色だったからだけど、
もしかしたら使用する色を変更出来たのかも知れないなあ。
円周率とかフラクタルだとか、バタフライエフェクト…
なんかそういうのにすごくワクワクするけど、同時になんだか怖い。
怖いっていうのは理解出来ないからなんだけど、でも理解しようにも頭が足りんようだ。
だから、遠くから眺めていようと思う。( ・ω・)じー
Re: 家に帰ればすぐさま勉強だ（サァ〜クセス・サァ〜クセス）
それはとっても嬉しいなって |
返信 |
Reply 思考の泡 ばか | |
まだひっぱります。
工作機械には、精度の限界となる数値を喰わせる、とします。それしかないので。
当然、理屈では、やっぱり、均等ではありません…寸分違わず図面どおりにできあがるなら。
でも、作る時の誤差で、うっかり、ほんとに均等にできちゃってる製品が、もしかしたら混じってるかもしれない。
そしてそれは、実は、自分が今使ってるこのこいつがそうなのかもしれない。みんな気付いてないだけで、そんな個体に巡り逢えているのかもしれない。
本当のことは誰にもわからないけど、美しいものはみんなの心の中にあるから。信じていれば、いつでもいっしょにいられる。
それはとても素敵だ、って思いました。
円周率がぴったり3の世界 |
返信 |
Reply | |
先日Googleさんも祝ってたオイラーの等式：(Wolfram Alphaさんありがとう)
はどうなるのかなー
えーとえーと、π=３ならiはともかくeも厳密値的に求まるはずだから…
…あれ？数学の世界、全部崩壊するんじゃね？
Re: バカが露見するのを覚悟の上で書く
…いつから…円周がキリのいい数字だと…勘違いしていた…？ |
返信 |
Reply | |
円の中心をぐるっと一回りした角度は2π(パイ)、そもそも整数で割り切れるものじゃありませんので…
深く考えたら負けですよー(弧度法＝いわゆるラジアン)
ヘリコプターの場合：
カワサキ OH-1
AH-64D アパッチ・ロングボウ
Re: バカがお答えします
家に帰ればすぐさま勉強だ（サァ〜クセス・サァ〜クセス） |
返信 |
Reply | |
とりあえずイラレで正七角形を生成して360/7度で回転させてみたことはナイショの話。
>「削ったり型を作ったりするときにどういう数値を工作機械に喰わせんだよコラ」
そうそう、結局そこなんですよね。理屈では図形として正七角形があり得るのはわかるのですが、
それを物体として切り出す過程がわからない。成型業界の人はいませんか。
実はこの業界の人は自分たちと違う尺度の単位を使っているとか。超極秘事項の。
きっと割り切れる円周率とか隠し持ってる。
つか、自分同等のﾅｶ~ﾏがいて安心した＞知恵袋。いや、そうじゃないだろ自分。
Re: バカが露見するのを覚悟の上で書く
バカがお答えします |
返信 |
Reply | |
・軸がぶれることに関しては、重さで調整するという手もあるとは思います。
・実は、円周が140cmとかなんです、多分。
・線分ををいくつかに等分することはわけなくできるので、
http://www.nmri.go.jp/eng/khirata/mechdesign/ch03/ch03_ap01.html
という手があるようです。
・気になってるのはそこではなくて「削ったり型を作ったりするときにどういう数値を工作機械に喰わせんだよコラ」ということじゃないかと思うんですが、実際のところ、そしてあくまで今のところ、人間の英知を結集して作れる円い物体って、正確さとしては円周率の小数点以下せいぜい数桁程度らしいです。回してる物自体がそもそも円ですらない。
なので、それでもなんとかなってるんだから、仮に軸がぶれてくるとしても、その前に他んとこが壊れるんじゃないかと。
以下蛇足。
…でも、個人的には、7本スポークの5穴は見ててなんとなく気持ち悪い部分もあります。
なんでぴったりのとこにしないの？とか、穴を開けて弱くなる位置があるんじゃないの？とか。
8本4穴や6本6穴ならある意味すっきりはするんです。もっともこれ言い出すとタイヤに空気入れる場所がなくなりますけども。
と思ってたら
http://okwave.jp/qa/q3707185.html
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1414702099
「へぇ、あんたもナナって言うんだ」
〜 7 について、ナナ（アイスクライマー）
蛇足2。
車のハンドル。
ハンドルを軸に止めるネジが真ん中1本、ということはよくあると思いますが、あれもなんとなく気持ち悪くて。
なんか、外れそうじゃない？その車が新車で最初に乗ってカーブ曲がるとき、まずは右カーブからじゃないとネジ緩みそうじゃない？
…丸棒に丸いのをただ嵌めてるわけないので、だいじょうぶなのは知ってはいるんですけどね。
バカが露見するのを覚悟の上で書く |
返信 |
とか、
こういうの
を見ていると、そこはかとなく不安になるんです。
だって、360は7で割り切れないんですよ？
いったいこの７本とか７枚とかは、何を持って『均等に配置されている』ことになっているんですか？
実はどこか１間隔、他と違って広かったり狭かったりしてないのですか？
高速で回転することを使命としているのに、実はほんのわずか均等さが欠如していて、
長い目で見たときに軸がぶれたり軸がぶれたり、軸がぶれたりすることはないんですか。
すんげぇ昔から謎に思っていたんですが、今回初めて口にしてみたのです。
頭のいい方からの冷ややかな目線なしでの回答をお待ちしています。